billiards
This is an open-source project bringing unsophisticated billiards physics written in typescript to the browser. Play pool, snooker, or 3-cushion online right here.
Features
- Backspin, sidespin an cushion bounces well modeled.
- Presentation using WebGL in any modern browser on mobile, linux, mac or windows.
- Record and playback breaks.
- Two player online mode with nchan nginx server.
- Nine ball, snooker and three cushion billiards rules.
- Deploys to github pages, vercel.com and render.com with github actions.
Online Demo
Demos run in all major desktop and mobile browsers and uses WebGL
- Nine ball ⬀ make a break and share replay link with friends
- Three cushion billiards ⬀ the ultimate test of physics and player (average on both counts)
- Snooker ⬀ we await the first 147 submission to the leaderboard.
- 4-ball Straight pool ⬀.
- Inspect physics and tweak constants using diagrams.
- Try to get on the leaderboard of highest breaks hosted on vercel.com
- Try two player online lobby using nchan
Reference material
- Papers on ball mechanics Han 2005 with important corrections by Kiefl.
- cushions, max spin, simulation and constants 1 2 3 4 5
- 3D graphics uses three.js
- Inline LaTeX editor for equations in README.md
Key equations
Based on Han 2005 paper
surface velocity
sliding motion
| 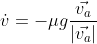 |
| 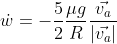 |
rolling motion
| 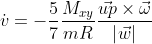 |
| 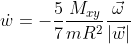 |
where
,
collisions
Based on paper by Alciatore incorporating throw effect due to the small amount of friction between balls. Figures to prove consistency between the code and paper here.
For ball $a$:
For ball $b$:
Where:
The relative velocity at the point of contact is computed as:
$\vec{v}_{\text{rel}} = (\vec{v}_a - \vec{v}_b) + \vec{r}_a \times \vec{\omega}_a - \vec{r}_b \times \vec{\omega}_b$
$\vec{v}_{\text{slip}}$ = $\vec{v}_{\text{rel}}$ - $(\vec{v}_{\text{rel}} \cdot \hat{n}) \hat{n}$
$\vec{r}_a = -R \cdot \hat{n}$ and $\vec{r}_b = R \cdot \hat{n}$
$J_{\text{normal}} = \frac{-(1 + e)v_{\text{rel,normal}}}{(2/m)}$
$J_{\text{tangential}} = \min\left( \frac{\mu J_{\text{normal}}}{v_{\text{rel}}}, \frac{1}{7} \right)(-v_{\text{rel,tangential}})$
$\hat{n}$: normal unit vector along the line of centers.
$\hat{t}$: tangential unit vector perpendicular to $\hat{n}$.
cushion bounce
This is based on a paper by Mathaven. Many of the figures from the paper are recreated to confirm correctness.
Slip velocity at cushion contact point I
\[ẋ_I = \dot{v_x} + \dot{\omega_y} R \sin \theta - \dot{\omega_z} R \cos \theta \qquad ẏ'_I = -\dot{v_y} \sin \theta + \dot{\omega_x} R\] \[\phi = \arctan\left(\frac{ẏ'_I}{ẋ_I}\right) \qquad s = \sqrt{(ẋ_I)^2 + (ẏ'_I)^2}\]Slip velocity at table contact point C
\[ẋ_C = \dot{v_x} - \dot{\omega_y} R \qquad ẏ_C = \dot{v_y} + \dot{\omega_x} R\] \[\phi' = \arctan\left(\frac{ẏ'_I}{ẋ_I}\right) \qquad s' = \sqrt{(ẋ_C)^2 + (ẏ_C)^2}\]Numerical solutions for the centroid velocity of the ball during compression and resititution phases.
\[(\dot{v_x})_{n+1} - (\dot{v_x})_n = - \frac{1}{M} \left[\mu_w \cos(\phi) + \mu_s \cos(\phi') \cdot (\sin \theta + \mu_w \sin(\phi) \cos \theta)\right] \Delta P_I\] \[(\dot{v_y})_{n+1} - (\dot{v_y})_n = - \frac{1}{M} \left[ \cos \theta - \mu_w \sin \theta \sin \phi + \mu_s \sin \phi' \cdot \left( \sin \theta + \mu_w \sin \phi \cos \theta \right) \right] \Delta P_I\]Numerical solutions for angular velocity of ball
\[(\dot{\omega_x})_{n+1}−(\dot{\omega_x})_n = -\frac{5}{2MR}[\mu_w \sin(\phi) + \mu_s \sin(\phi') \times (\sin(\theta) + \mu_w \sin(\phi)\cos(\theta))]\Delta P_I\] \[(\dot{\omega_y})_{n+1}−(\dot{\omega_y})_n = -\frac{5}{2MR}[\mu_w \cos(\phi)\sin(\theta) - \mu_s \cos(\phi') \times (\sin(\theta) + \mu_w \sin(\phi)\cos(\theta))]\Delta P_I\] \[(\dot{\omega_z})_{n+1}−(\dot{\omega_z})_n = \frac{5}{2MR}(\mu_w \cos(\phi)\cos(\theta))\Delta P_I\]$\theta$ is a constant of the angle of cushion contact above ball centre with $\sin(\theta) = 2/5$. $μ_s$ is the coefficient of sliding friction between the ball and table surface. $μ_w$ is the coefficient of sliding friction between the ball and the cushion.
Work done by the normal force at contact point $I$ along the $Z’$-axis which is aligned from the ball centre to I
\[W_{Z'}^I(P_I^{(n+1)}) = W_{Z'}^I(P_I^{(n)}) + \frac{\Delta P_I}{2} \left( z'_I(P_I^{(n+1)}) + z'_I(P_I^{(n)}) \right)\]The ball is assumed to be bouncing in the +y cushion. Compression phase iterates until
\[\dot{v_y} <= 0\]For the restitution phase the iteration continues until the work done is
\[W_{Z'}^I >= (1 - e_e^2) W_{compression}\]Some of the Mathaven equations not supplied by the paper were inferred by LLMs and the code for them was initially generated by a combination of Claude, Qwen and GPT-4o.
Useful commands
Install
nvm use v22.12.0
yarn install
yarn dev
yarn gltfpack
This generates artefacts in /dist for prod deployment (e.g. on github static pages)
Run
yarn serve
Then open http://localhost:8080/ in your browser to play
Test
yarn test
yarn coverage
Maintain
yarn deps
yarn upgrade -L
yarn prettify
Two player
yarn serve
then open http://localhost:8080/multi.html to see options, message server is public nchan.
Controls
Use mouse, touch screen or keyboard:
⇦ ⇨ Aim
Control ⇦ ⇨ Fine aim
⇧ ⇩ Topspin and backspin
Shift ⇦ ⇨ Side spin
Space Hit - hold for more power
Progress snapshots
July 2018

July 2019
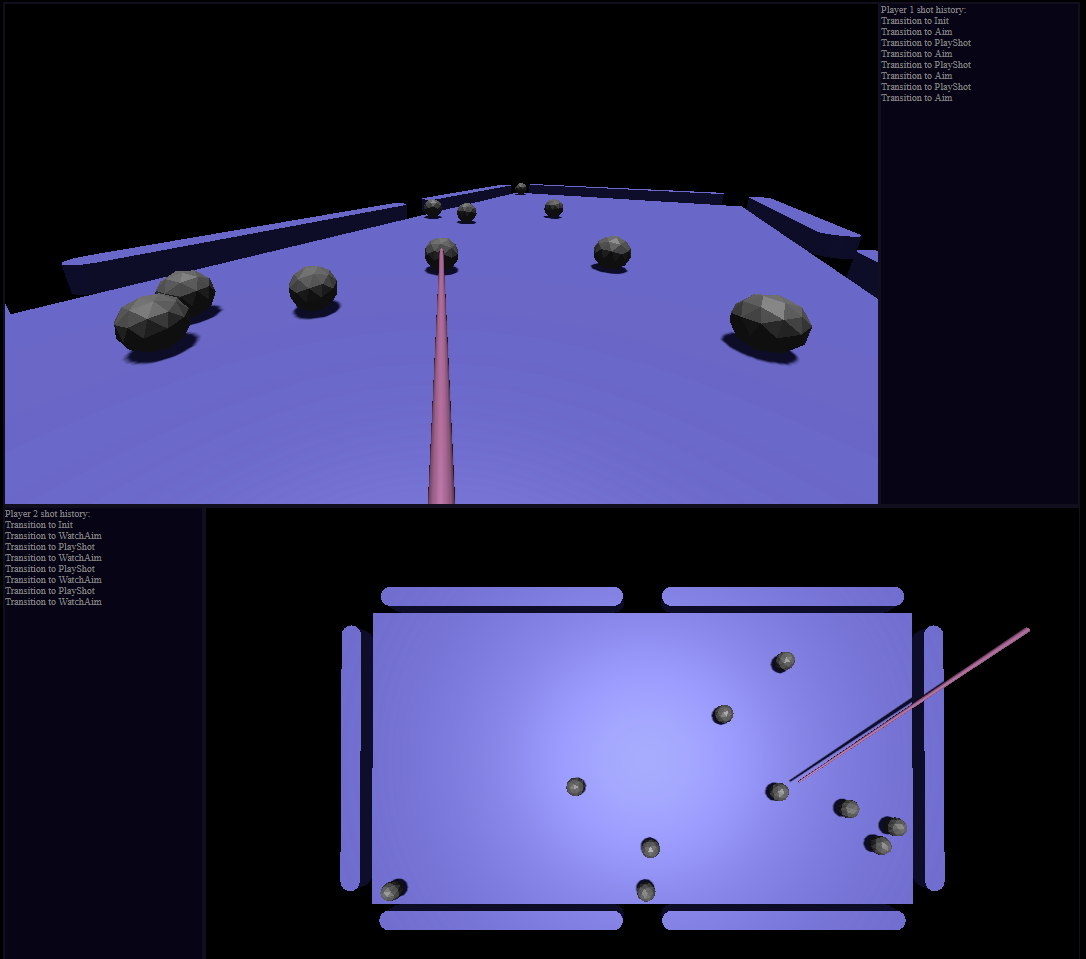
March 2021
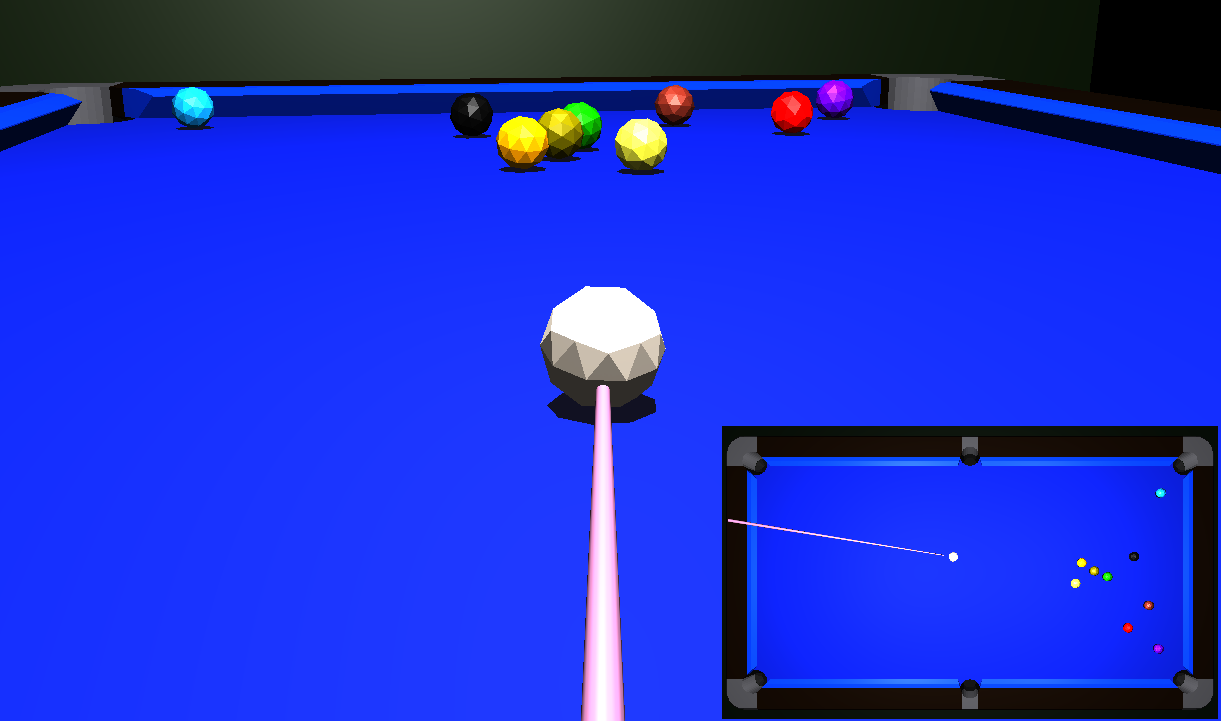
August 2023 (mobile)
| top | aim |
|---|---|
|  |  |
Star History
Licence
This project is open source and licensed under the GNU General Public License - see the LICENSE file for details. Contributions welcome.

